More Discussion On Least Squares Loop Closure

by Larry Fish

Many months ago I wrote an article describing some problems I had found in cave survey programs using Least Squares to close loops. Since then, there have been two rebuttal articles focusing on my program, COMPASS, as a way of proving the efficacy of Least Squares. I think it is now time to return to the original topic of discussion, Least Squares.

MOST CAVE SURVEY PROGRAMS DO LEAST SQUARES WRONG.

In the course of this discussion, I received a series of letters from John Halleck. John is extremely knowledgeable about surveying mathematics and he has given me some very interesting insights into the Least Squares issues.

I had always assumed that the cave survey programs that used Least Squares were written correctly, so I assumed that the problems I was seeing were due to flaws in Least Squares itself. John pointed out that these problems were actually due to the fact that most cave survey programs leave out important steps when they do Least Squares.

Most Least Squares cave survey programs are based on an old article that appeared in the NSS Bulletin in 1970 written by V. A. Schmidt and J.H. Schelleng. John says that this article was intended to be a simplified introduction to the topic of Least Squares loop closure. These simplifications make the technique unsuitable for dealing with blunders. Thus, any program that uses the Schmidt and Schelleng technique will have trouble handling blunders.

WEIGHTS AND LEAST SQUARES

The problem with the Schmidt and Schelleng technique is the way it deals with weights. Weights are used by Least Squares to compensate for parts of a survey where the data is less reliable. The weights work by controlling how the program processes different parts of the survey. If the weights are high, the program assumes this part of the data is good and will favor it when it closes the cave. Likewise, if the weights are low, the program assumes the data is poor and will not rely as heavily on this part of the survey.

For Least Squares to work properly, the weights must track the quality of the data. Unfortunately, the simplifications built into Schmidt and Schelleng do not do this.

ASSIGNING WEIGHTS IN LEAST SQUARES.

There are two things that can make the data in a cave survey unreliable: Random Errors and Blunders. Let's look at how weights can be derived to deal with both.

1. Random Errors. Random errors are generally small errors that occur during the process of surveying. They result from the fact that it is impossible to get absolutely perfect measurements each time you read a compass, inclinometer or tape measure. For example, your hand may shake as you read the compass, the air temperature may affect the length of the tape, and you may not aim the inclinometer precisely at the target.

One important aspect of Random Errors is that they obey statistical laws and, as a result, we can predict how big they should be for a series of survey shots. For example, if we know that a compass has a one degree uncertainty in its measurements, we can project this uncertainty through a series of survey shots. This gives us a projection of the amount of error there should be in the data if the errors are random. This information can be used to derive a set weights for the data.

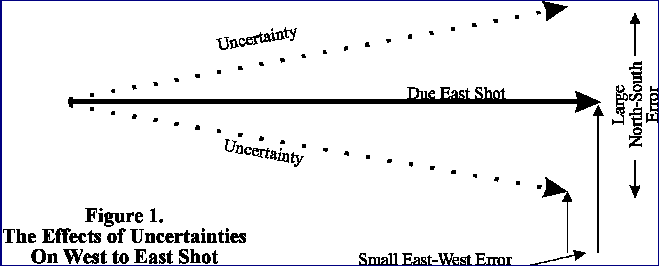
A key part of this projection is the fact that the uncertainty of the instruments effects different shots in different ways. For example, if you have a two degree compass error in a shot that is bearing north, most of the error will show up in the east-west direction. Likewise, on an eastward shot, most of the error will be in the north-south direction. This is particularly important for cave surveys, because cave passages tend to be oriented along joints and faults that make the passages run in particular directions. This can have a strong effect on the way random errors accumulate. For example, a narrow north-south oriented loop would have a different pattern of errors than a similar east-west oriented loop.

This is one of the places where Schmidt and Schelleng simplified things. They derive the initial weights based upon shot length. They just assumed longer shots would have more error and so they assign lower weights to long shots. This simplification has problems because it ignores the differing effects that each instrument has on the errors. It also ignores the way in which the direction of the shot effects the errors.

Assigning weights correctly is important for several reasons. First, if the weights are not correct, the closure cannot be correct because the program will be compensating in the wrong places. Second, the fact that our projections are wrong may cause us to miss some blunders or find other blunders that are not real.

2. Blunders. After we have adjusted the survey data using weights derived from the projected errors, we can check to see how closely the projected errors match the real errors. (You can do this by looking at the amount of adjustment the program had to do to close the survey.) If the actual errors are greater than the projected errors, it probably means that there are blunders in the data.

Blunders are important because they have very different properties than random errors. Blunders are fundamental errors in the surveying process like reading the wrong end of the compass or writing down the wrong numbers. Blunders are different because they don't obey statistical laws and cannot be predicted in the same way as random errors. This is important because Least Squares is based on the assumption that the errors in the data are random. Likewise, the way weights are generated in Least Squares is based on our ability to predict random errors. If the data has a blunder in it, these assumptions are will not work and we have to take some extra steps in the closure process.

If we adjust a survey and find that the our predictions do not match the actual errors, we can use this information to derive a new set of weights that compensate for the blunders. Then, because the weights are based on the actual errors versus the expected errors, the weights compensate for blunders in the data. Thus, blundered data will have a low weight and the effect will be confined to a small part of the cave and not spread to nearby passages. This is the part that Schmidt and Schelleng and most cave survey programs miss.

Since Bob Thrun has presented his program as an example of the superiority of Least Squares, we should look at how his program assigns weights. Looking at his distributed software, you find that he has several options for assigning weights. These include the number of shots, the shot length, the standard deviation and the variance. The first two, the number of shots and the shot length, do not predict errors based on how each instrument's uncertainty effect the error. The other two options, standard deviation and variance, do take into account the individual instrument's contribution to the error. However, the methods have been simplified so they do not take into account the orientation of the shots. Finally, the most important problem is that the program does not compare the actual errors with the predicted errors and, if necessary, derive a new set of weights. For this reason, the program cannot deal with blunders in a mathematically correct way.

To summarize, if Least Squares is done correctly, it will deal with blunders as effectively as any other technique. Further, the whole argument about sequential versus simultaneous closures is a red herring. According to John, there are sequential methods for adjusting least squares surveys that compute EXACTLY the same solution as a simultaneous adjustment of the data. The problem is that few cave survey programs do Least Squares correctly.

HOW TO KNOW IF A PROGRAM IS IMPLEMENTED CORRECTLY.

How can you tell if a program implements Least Squares correctly? Without examining the computer code it is difficult to tell, but there are some clues. Here is a list:

1. Schmidt And Schelleng. Any program that is based on Schmidt and Schelleng is suspect unless it uses a different method of deriving the weights. Since Schmidt and Schelleng uses the inverse of the shot length to derive weighting factors, any program that uses this technique is also wrong. Even if the program uses a different method, it has to satisfy two criteria before it is correct. First, it must assign initial weights based on the errors in the individual instruments and on the orientation of the shot. Second, if data proves to contain blunders, it must assign a new set of weights based on analyzing both the projected errors and the actual errors.

2. Instrument Uncertainties. In order to predict the expected error for a loop, you must estimate the size of the typical error you would find with each survey instrument. For example, if you know that your compass has a 0.5 degree error, you can easily project how big the error should be at end of particular survey loop. Since the quality of instruments can vary, you would expect that a correctly implemented program would allow you enter error values for the instruments. This is not completely reliable. For example, a program might set these values internally and still implement Least Squares correctly. Likewise, a program might allow you to enter error values and not use them properly.

3. Test Blunders. I first discovered the problems with poorly implemented Least Squares when I wrote a program based on Schmidt and Schelleng and found that it smeared a large blunder in Groaning Cave all over the map. One way to tell if a program has properly implemented Least Squares is to insert a blunder in a survey with lots of loops and see if adjacent loops are distorted.

4. Use A Rotated Test Cave. A program that uses the proper method of weighting will compensate for the direction of the shots. This means that you should be able to rotate all the measurements in a survey and still produce the same closure. For example, you should be able to add 45 degrees to all the azimuths and still have the plot appear identical to the unrotated version except rotated by 45 degrees. This is a bit more difficult to set up, but you could plot the images on paper and then test by superimposing and rotating the images.

FURTHER INFORMATION.

I have deliberately steered away from the mathematical aspects of the problem in this article, but these concepts are based upon well-established principles in land surveying. One thing John has pointed out is that these problems were solved decades ago by land surveyors. John is working on an article that includes a detailed mathematical and theoretical discussion of the topic and sample code. For those of you that want to delve deeper into the subject, John has related articles and a good introductory bibliography at:

http://www.cc.utah.edu/~nahaj/cave/survey/